Introdução à Computabilidade e Complexidade

Autor

Márcio Nicolau

Data de Publicação

4 de agosto de 2025

Objetivos da Aula

  • Apresentar a disciplina e seu contexto na Ciência da Computação
  • Compreender a importância do estudo dos limites da computação
  • Conhecer os principais tópicos que serão abordados no curso

Conteúdo

1. O que é Teoria da Computação?

A Teoria da Computação é um ramo fundamental da Ciência da Computação que investiga, de forma formal, as capacidades e limitações dos sistemas computacionais. De acordo com Sipser (2012), a área organiza-se em torno de três questões centrais e interconectadas e apoia-se na tese de Church–Turing, que propõe que a noção informal de “algoritmo efetivo” é capturada pelos modelos formais de computação (como Máquinas de Turing e cálculo lambda).

  1. O que significa um problema ser “resolvível” por um computador?
    • A Teoria da Computação estabelece os limites teóricos do que pode ser computado, independentemente da tecnologia. Em Sipser (2012), problemas são tipicamente formulados como linguagens (conjuntos de cadeias) e “resolver” um problema significa decidir a linguagem correspondente. Máquinas de Turing modelam algoritmos e permitem classificar linguagens em decidíveis (computáveis) e indecidíveis. O problema da parada é o exemplo clássico de linguagem indecidível. Também são estudadas linguagens reconhecíveis (recursivamente enumeráveis), nas quais existe um algoritmo que aceita todas as cadeias da linguagem, mas pode não terminar para cadeias fora dela.
  2. Quão eficientemente um problema pode ser resolvido?
    • Para os problemas decidíveis, mede-se o custo de recursos (tempo e espaço). Sipser (2012) define classes de complexidade como P (decisão em tempo polinomial por MT determinística) e NP (decisão com verificador polinomial/certificado polinomial). Estudam-se ainda coNP, PSPACE e EXP, entre outras. Reduções polinomiais (\(\leq_p\)) relacionam problemas quanto à dificuldade; problemas NP-completos (por exemplo, SAT via Teorema de Cook–Levin) são os “mais difíceis” de NP no sentido de que qualquer problema de NP reduz-se a eles por uma redução polinomial.
  3. Quais são os modelos matemáticos de computação e como eles se relacionam?
    • A teoria explora modelos como autômatos finitos (DFA/NFA), autômatos com pilha (PDA), gramáticas (livre de contexto, regulares), Máquinas de Turing e funções recursivas. Resultados centrais incluem equivalência entre variantes razoáveis de Máquinas de Turing (fitas múltiplas, não determinismo polinomialmente simulável) e a correspondência entre classes de linguagens e modelos (por exemplo, linguagens regulares \(\leftrightarrow\) DFA/NFA; livres de contexto \(\leftrightarrow\) PDA). Essas relações ajudam a escolher o modelo adequado para cada classe de problemas.

Fundamentos Matemáticos

A Teoria da Computação está profundamente enraizada em lógica, conjuntos e prova matemática. Em Sipser (2012), conceitos como linguagens formais, gramáticas e autômatos são fundamentais. Técnicas como diagonalização, contagem, hierarquias de linguagens (Chomsky) e propriedades de fechamento (união, concatenação, estrela de Kleene) são usadas para demonstrar capacidades e limites de modelos. Lemas de bombeamento (para linguagens regulares e livres de contexto) ajudam a provar que certas linguagens não pertencem a uma classe específica.

Limites da Computação

Um dos resultados mais profundos é a existência de problemas indecidíveis — não há algoritmo que resolva todos os casos. Além do problema da parada, Sipser (2012) apresenta famílias inteiras de problemas indecidíveis por meio de reduções (many-one) e teoremas como o de Rice, que mostra que qualquer propriedade semântica não trivial de linguagens reconhecidas por Máquinas de Turing é indecidível.

Complexidade Computacional

Além de decidir computabilidade, a teoria estuda eficiência. Em Sipser (2012), P costuma ser associada a “tratável” (embora haja nuances práticas), enquanto NP-completude caracteriza problemas para os quais não se conhece algoritmo polinomial, mas cuja verificação é polinomial. A relação entre classes forma uma cadeia clássica de inclusões P \(\subseteq\) NP \(\subseteq\) PSPACE \(\subseteq\) EXP, com várias questões em aberto — a mais famosa é se P \(=\) NP.

Aplicações Práticas

Embora teórica, a área tem impacto direto: teoria de autômatos fundamenta análise léxica/regex e parsers; resultados de complexidade orientam escolhas de algoritmos e reconhecem limites (por exemplo, projetar heurísticas/aproximações para NP-difíceis); indecidibilidade informa o desenho de analisadores estáticos. SAT/SMT solvers e métodos formais são aplicações centrais de ideias de verificabilidade e redução.

Segundo Sipser (2012), dominar esses conceitos fornece ferramentas para avaliar viabilidade, projetar algoritmos e reconhecer fronteiras fundamentais do que a computação pode (e não pode) alcançar.

NotaDefinições e Exemplos Canônicos

Definições essenciais (ver Sipser (2012)):

  • Decidível (computável): existe uma Máquina de Turing que decide a linguagem (aceita cadeias da linguagem e rejeita as demais, sempre parando).
  • Reconhecível (recursivamente enumerável): existe uma MT que aceita todas as cadeias da linguagem; para cadeias fora dela, pode rejeitar ou não parar.
  • Redução polinomial (\(\leq_p\)): problema A reduz-se a B se existe transformação computável em tempo polinomial que mapeia instâncias de A em instâncias de B preservando respostas; se B tem algoritmo polinomial e A \(\leq_p\) B, então A também tem algoritmo polinomial.
  • NP-completo: problemas em NP aos quais todo problema de NP reduz-se por \(\leq_p\). São os “mais difíceis” de NP; se um NP-completo tiver algoritmo polinomial, então P \(=\) NP.

Exemplos canônicos de NP-completos:

  • SAT e 3-SAT (Cook–Levin): satisfatibilidade booleana em CNF (3-SAT com 3 literais por cláusula).
  • CLIQUE: dado grafo G e k, existe um conjunto de k vértices todos adjacentes entre si?
  • VERTEX-COVER: dado G e k, existe conjunto de k vértices que cobre todas as arestas?
  • INDEPENDENT-SET: dado G e k, existe conjunto de k vértices sem arestas entre si?
  • HAMILTONIAN-CYCLE: existe ciclo simples que visita todos os vértices exatamente uma vez?

Observação: muitos desses problemas reduzem-se entre si em tempo polinomial, formando uma teia de equivalências quanto à dificuldade dentro de NP (ver mapas de reduções em Sipser (2012)).

Diagrama: Hierarquia de Classes (visão teórica)

graph TD
    P[P] --> NP[NP]
    P --> coNP[coNP]
    NP --> PSPACE[PSPACE]
    coNP --> PSPACE
    PSPACE --> EXP[EXP]

    %% Notas
    note1["Inclusões conhecidas:
    P ⊆ NP, P ⊆ coNP,
    NP ⊆ PSPACE,
    PSPACE ⊆ EXP"]
    note2["Questões em aberto:
    P ?= NP,
    NP ?= coNP"]

    P -.-> note1
    NP -.-> note2
Figura 1: Hierarquia de Classes (visão teórica). Simbolo ?= (\(\stackrel{?}{=}\)) indica que a igualdade é uma questão aberta. Fonte: Sipser (2012).

Mini-exercício

  1. Explique em alto nível a redução de 3-SAT para CLIQUE: descreva como mapear cláusulas para camadas do grafo, literais para vértices e como definir arestas entre literais compatíveis. Indique o valor de k.
  2. Classifique cada afirmação como verdadeira ou aberta (desconhecida):
    • P \(\subseteq\) NP
    • NP \(\subseteq\) PSPACE
    • P \(=\) NP
    • NP \(\subseteq\) coNP
    • P \(\subset\) EXP
DicaGabarito resumido
  1. 3-SAT → CLIQUE (esboço): para uma fórmula CNF com m cláusulas, crie um grafo com uma camada por cláusula; crie um vértice por literal em cada cláusula. Conecte vértices de camadas diferentes se os literais forem compatíveis (não contraditórios). Defina (\(k = m\)). Há um clique de tamanho m sse a fórmula é satisfatível (escolhe-se um literal por cláusula, todos compatíveis).
  2. Classificações:
    • P \(\subseteq\) NP — verdadeira
    • NP \(\subseteq\) PSPACE — verdadeira
    • P \(=\) NP — aberta
    • NP \(\subseteq\) coNP — aberta
    • P \(\subset\) EXP — verdadeira (pela hierarquia de tempo)

Gráfico das Classes de Complexidade

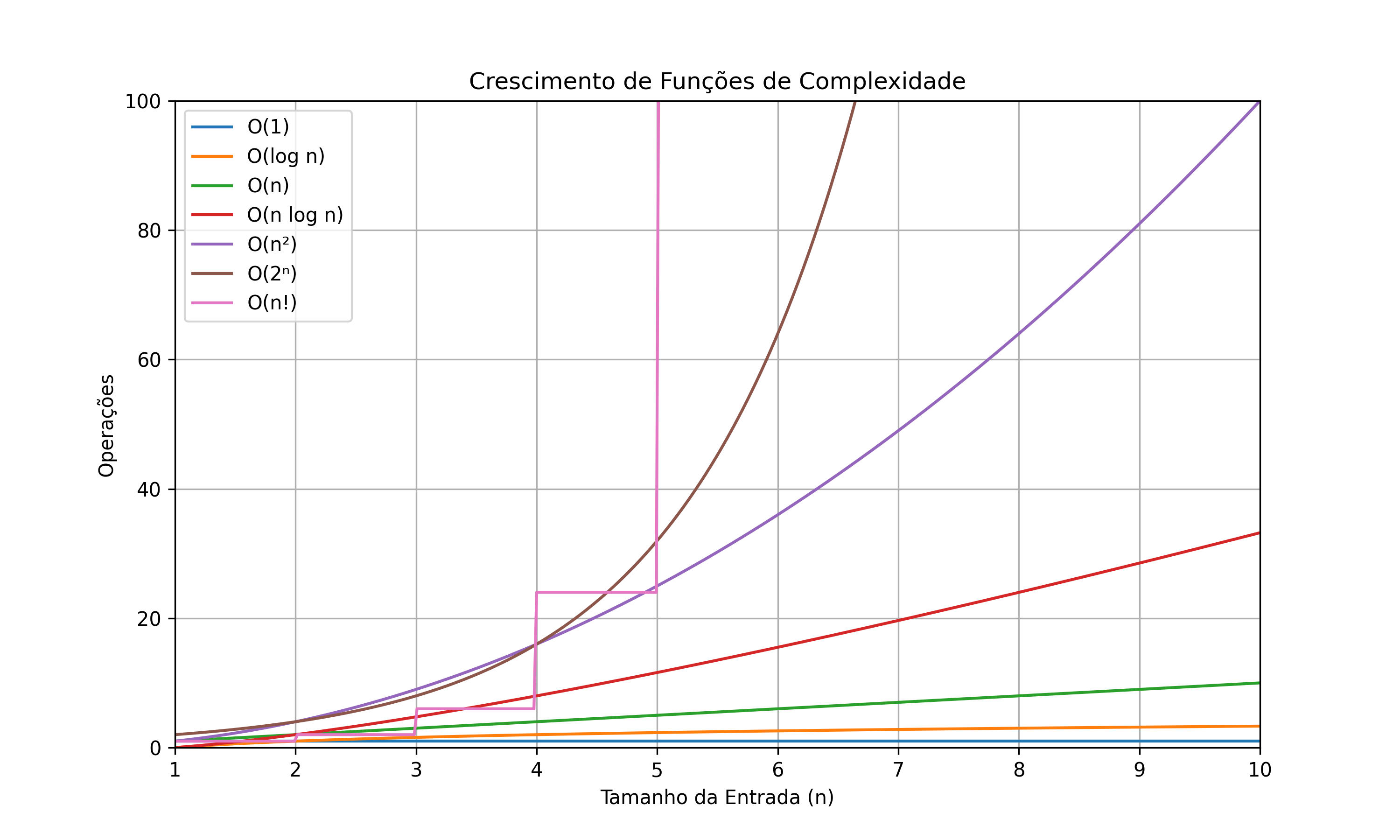
Figura 2: Classes de Complexidade em relação ao tamanho da entrada.

2. Por que estudar Computabilidade e Complexidade?

O estudo da Computabilidade e Complexidade não é apenas um exercício teórico, mas uma base essencial para qualquer profissional de ciência da computação. Sipser (2012) destaca várias razões fundamentais para sua importância:

1. Compreensão dos Limites Fundamentais

A Teoria da Computação estabelece fronteiras claras sobre o que pode e o que não pode ser resolvido por computadores. Por exemplo, o Teorema da Incompletude de Gödel e o Problema da Parada de Turing demonstram que existem problemas que estão além da capacidade de qualquer sistema computacional, independentemente de sua potência. Compreender esses limites: - Evita a busca por soluções impossíveis - Ajuda a identificar quando um problema precisa ser reformulado - Fornece uma base para a análise de problemas computacionais

2. Desenvolvimento de Raciocínio Lógico-Matemático

O estudo formal da computação desenvolve habilidades de pensamento abstrato e rigor lógico que são valiosas em todas as áreas da computação. Através de provas formais e argumentação lógica, os estudantes aprendem a: - Estruturar problemas de forma clara e precisa - Construir argumentos lógicos rigorosos - Identificar falhas em raciocínios complexos - Aplicar métodos formais para análise de algoritmos

3. Aplicações Práticas em Diversas Áreas

Embora altamente teórica, a Teoria da Computação tem aplicações práticas em:

Segurança da Informação - Protocolos de criptografia baseiam-se em problemas computacionalmente difíceis - A segurança do RSA, por exemplo, depende da dificuldade de fatoração de números grandes

Inteligência Artificial - Compreensão dos limites do aprendizado de máquina - Análise da complexidade de algoritmos de IA - Estudo da capacidade de aprendizado de diferentes modelos

Engenharia de Software - Análise de complexidade de algoritmos - Verificação formal de programas - Otimização de compiladores

Ciência de Dados - Análise da complexidade de algoritmos de processamento de dados - Limites da capacidade de processamento de grandes volumes de dados

4. Impacto na Indústria de Tecnologia

Grandes empresas de tecnologia como Google, Microsoft e Amazon empregam teóricos da computação para: - Desenvolver algoritmos mais eficientes - Resolver problemas complexos de escalabilidade - Garantir a segurança de sistemas distribuídos - Otimizar o uso de recursos computacionais

5. Base para Pesquisa Avançada

O estudo da Teoria da Computação é fundamental para pesquisas em: - Criptografia quântica - Computação quântica - Algoritmos distribuídos - Teoria da informação - Complexidade descritiva

Como destaca Sipser (2012), “a teoria da computação é o estudo do poder e das limitações da computação”. Seu estudo não apenas enriquece nossa compreensão teórica, mas também fornece as ferramentas necessárias para enfrentar os desafios práticos da computação moderna.

AvisoDesafio: Implementando um Algoritmo de Busca

Vamos implementar o algoritmo de busca binária. Complete a função busca_binaria abaixo:

def busca_binaria(lista_ordenada, alvo):
    """
    Implemente a busca binária aqui.
    Retorne o índice do alvo na lista ou -1 se não encontrado.
    """
    # Seu código aqui
    pass
DicaDicas
  1. A busca binária requer que a lista de entrada esteja ordenada.
  2. Use dois ponteiros, um no início e outro no final da lista.
  3. Calcule o elemento do meio e compare com o alvo.
  4. Ajuste os ponteiros com base na comparação.
  5. Continue até encontrar o elemento ou esgotar a busca.

Instruções:

  1. Implemente a função busca_binaria no editor de código acima.
  2. A função deve receber uma lista ordenada e um valor alvo.
  3. Ela deve retornar o índice do alvo na lista, ou -1 se não for encontrado.
  4. Clique em “Executar Testes” para verificar sua implementação.
DicaDica

Lembre-se que a busca binária tem complexidade \(O(\log n)\) e assume que a lista de entrada está ordenada.

Mapa Conceitual do Curso

Figura 3: Mapa Conceitual do Curso: Computabilidade e Complexidade

Atividade Prática

Código Python 
# Exemplo simples de problema computacional
def is_prime(n):
    if n < 2:
        return False
    for i in range(2, int(n**0.5) + 1):
        if n % i == 0:
            return False
    return True

# Testando a função
print("Números primos até 10:")
for num in range(1, 11):
    if is_prime(num):
        print(f"{num} é primo")
Números primos até 10:
2 é primo
3 é primo
5 é primo
7 é primo
Figura 4

Diagrama: Hierarquia de Classes de Complexidade

graph TD
    P[Classe P] -->|Problemas resolvíveis em tempo polinomial| NP
    NP[Classe NP] -->|Problemas verificáveis em tempo polinomial| NP_Completo
    NP_Completo[NP-Completo] -->|Problemas NP-difíceis em NP| NP_Duro
    NP_Duro[NP-Duro] -->|Problemas pelo menos tão difíceis quanto NP| EXP
    EXP[Classe EXP] -->|Problemas resolvíveis em tempo exponencial| ...
Figura 5: Hierarquia de Classes de Complexidade

Exercícios

  1. Pesquise e descreva um problema prático que seja NP-Completo.
  2. Explique por que o problema da parada (halting problem) é importante na teoria da computação.
  3. Liste três áreas da computação que se beneficiam do estudo da complexidade computacional.

Referências Bibliográficas

SIPSER, Michael. Introdução à Teoria da Computação. 3. ed. São Paulo, Brasil: Cengage Learning, 2012.